Geodetic Bayesian Inversion Software – GBIS

Current release: Version 1.1

Last update: 08 August 2018

Download GBIS from here.

The open-source Geodetic Bayesian Inversion Software (GBIS, Version 1.1) allows the user to perform the inversion of Interferometric Synthetic Aperture Radar (InSAR) and/or Global Positioning System (GPS) data to estimate deformation source parameters. The inversion software uses a Markov-chain Monte Carlo algorithm, incorporating the Metropolis-Hastings algorithm [e.g., Hastings, 1970; Mosegaard and Tarantola, 1995], to find the posterior probability distribution of the different source parameters.

A detailed explanation of the inversion approach is provided in Bagnardi and Hooper [2018].

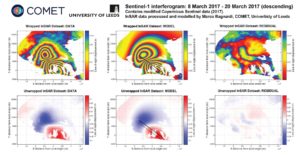
Modelling results from the inversion of InSAR data. The proposed model is composed of a horizontal sill intrusion at ~5 km depth (black rectangle) fed by a deflating source at ~6 km depth (black star).

The current version of GBIS includes analytical forward models for magmatic sources of different geometry (e.g., point source [Mogi, 1958], finite spherical source [McTigue, 1987], prolate spheroid source [Yang et al., 1988], penny- shaped sill-like source [Fialko et al., 2001], and dipping dike with uniform opening [Okada, 1985]) and for dipping faults with uniform slip [Okada, 1985], embedded in a isotropic elastic half-space. However, the software architecture allows the user to easily add any other analytical or numerical forward models to calculate displacements at the surface.

GBIS is written in Matlab and uses a series of third-party functions to perform specific steps for data pre-processing, subsampling, and includes forward models from the dMODELS software package [Battaglia et al., 2013].

The software offers a series of pre- and post-processing tools aimed at estimating errors in InSAR data, and at graphically displaying the inversion results.

GBIS is developed by Marco Bagnardi and Andrew Hooper.

A Google discussion group is available after registration at:

https://groups.google.com/forum/#!forum/gbisinfo

References

Bagnardi M. & Hooper A, (2018). Inversion of surface deformation data for rapid estimates of source parameters and uncertainties: A Bayesian approach. Geochemistry, Geophysics, Geosystems, 19.

 

Battaglia, M., Cervelli, P. F., & Murray, J. R. (2013). dMODELS: A MATLAB software package for modeling crustal deformation near active faults and volcanic centers. Journal of Volcanology and Geothermal Research, 254, 1-4.

Fialko, Y., Khazan, Y., & Simons, M. (2001). Deformation due to a pressurized horizontal circular crack in an elastic half-space, with applications to volcano geodesy. Geophysical Journal International, 146(1), 181-190.

Hastings, W. K. (1970). Monte Carlo sampling methods using Markov chains and their applications. Biometrika, 57(1), 97-109.

McTigue, D. F. (1987). Elastic stress and deformation near a finite spherical magma body: resolution of the point source paradox. Journal of Geophysical Research: Solid Earth, 92(B12), 12931-12940.

Mogi, K. (1958). Relations between the eruptions of various volcanoes and the deformations of the ground surfaces around them.

Mosegaard, K., & Tarantola, A. (1995). Monte Carlo sampling of solutions to inverse problems. Journal of Geophysical Research: Solid Earth, 100(B7), 12431-12447.

Okada, Y. (1985). Surface deformation due to shear and tensile faults in a half-space. Bulletin of the seismological society of America, 75(4), 1135-1154.

Yang, X. M., Davis, P. M., & Dieterich, J. H. (1988). Deformation from inflation of a dipping finite prolate spheroid in an elastic half‐space as a model for volcanic stressing. Journal of Geophysical Research: Solid Earth, 93(B5), 4249-4257.